In rectangular coordinates we find the area bounded by the curve
the x-axis, and the ordinates at
and
using 
The corresponding problem in polar coordinates is that of determining the area bounded by the curve
and the two radius vectors
and
In Fig. 4 this is the area bounded by the curve and the lines OA and OB.
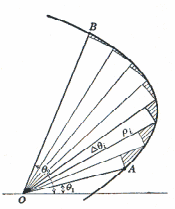
We divide the
-interval from
to
up into n subintervals (not necessarily equal) having the magnitudes
We then draw the corresponding radius vectors, denoting their lengths by
and draw the circular arcs as shown.
Remembering that the area of a circular sector having radius r and central angle
is
we write down the following expression for the sum of the areas of the circular sectors:
The area bounded by the curve and the lines OA and OB is then equal to the limit of the following sum
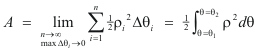
where we are requiring that the largest
as
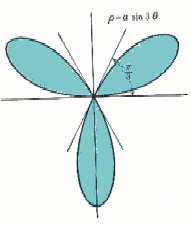
Example: Compute the area bounded by the curve
The shaded area is three times the area of one leaf:
