Finding Turning Points of Polar Curves

A turning point in cartesian coordinates is the solution toWe cannot form this expression in polar coordinates directly. If in polar coordinates we haveas a function ofthenandso nowandare expressed in terms of the angleand we can use the parametric formula for the gradient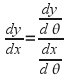to find the gradient at any point.

If we want a turning point then we solve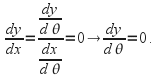From this we obtain value(s) forand can then useto obtain values for

ExampleFind the turning point.

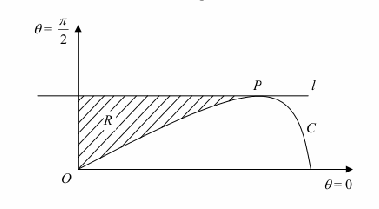
Clear all the factions by multiplying byand cancel the non zero constantobtaining

Divide throughout byto obtain

Now use the double angle formulato express everything in terms of

Clear all the fractions to obtain