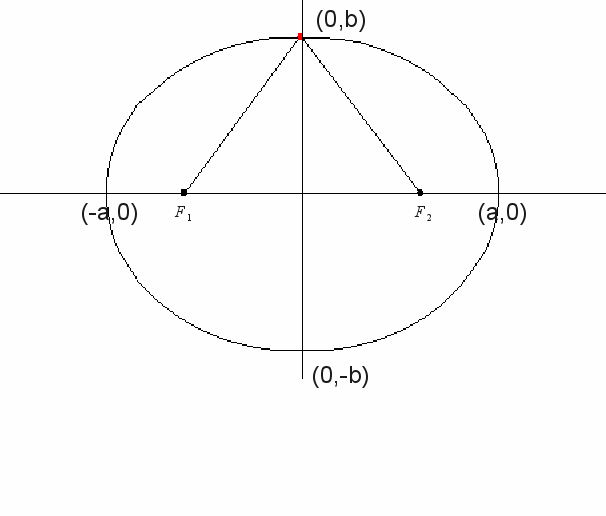
An ellipse may be defined geometrically in several different ways. One of these is that if the sum of the lengths of tow lines drawn from two points is made to eaqual a constant, the locus generates an ellipse. We may also define the ellipse by an equation:(x^-x-0)^2 over a^2 +(y-y-0)^2 over b^2 =1. The centre of the ellipse is at (x-0 , y-0) in this case.
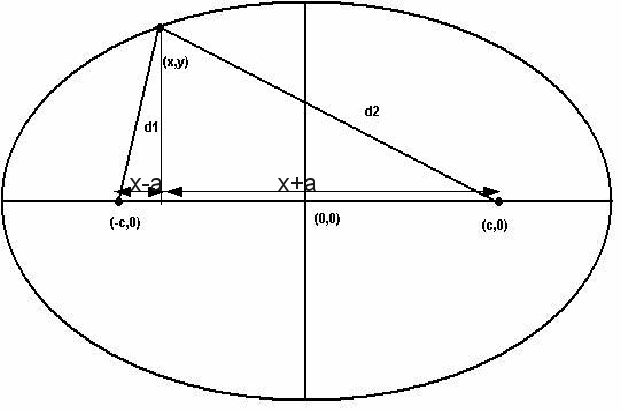
Square both sides
Square both sides:
Group like terms:
Divide by
Sub
to obtain