We often have to find analytic expressions for the trigonometric formulae![]() The method is illustrated in the following examples.
The method is illustrated in the following examples.
Example: Find an expression for![]()
If![]() then
then![]()
Multiply both sides by![]() to obtain
to obtain![]()
Now multiply both sides by 2 obtaining![]() and subtract
and subtract![]() from both sides to obtain
from both sides to obtain![]()
This is a quadratic expression in![]() so we can solve it using the ordinary quadratic formula.
so we can solve it using the ordinary quadratic formula.
![]() - remember that our quadratic is in terms of
- remember that our quadratic is in terms of![]()
![]()
Now take the natural logarithms of both sides to obtain
![]()
Since![]()
Example Find an expression for![]()
If![]() then
then![]() so
so![]()
Multiply both sides by![]() to obtain
to obtain![]()
Now multiply both sides by 2 obtaining![]() and subtract
and subtract![]() from both sides to obtain
from both sides to obtain![]()
This is a quadratic expression in![]() so we can solve it using the ordinary quadratic formula.
so we can solve it using the ordinary quadratic formula.
![]() - remember that our quadratic is in terms of
- remember that our quadratic is in terms of![]()
![]()
Now take the natural logarithms of both sides to obtain
![]()
Since![]()
Example Find an expression for![]()
If![]() then
then![]() so
so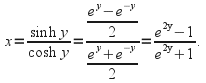
Multiply both sides by![]() to obtain
to obtain![]()
Expand the brackets:![]() and move the
and move the![]() term to the left, and the
term to the left, and the![]() term to the right, obtaining
term to the right, obtaining
![]()
Now factorise with![]()
Divide by![]()
Now take the natural logs of both sides and divide by 2.
![]()
