Loci Defined by Differences of Arguments

The equationdefines a locus of points. In fact it defines part of a circle. We can writeso that the locus is the set of pointswith a difference in the angle with the real axis ofbetween the lines drawn from the points andtorespectively.

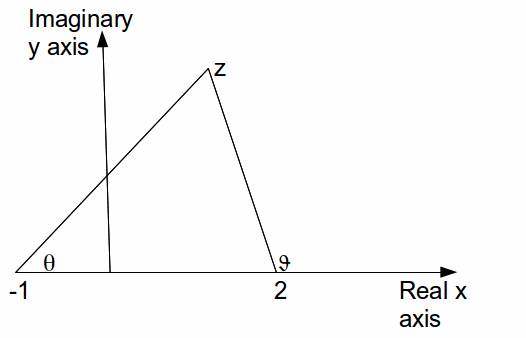
The argument offromisand the argument offromisso thatWe can find the angle formed atby the lines to -1 and 2 on the real axis in terms ofand

Draw a vertical line fromand label angles as shown below.

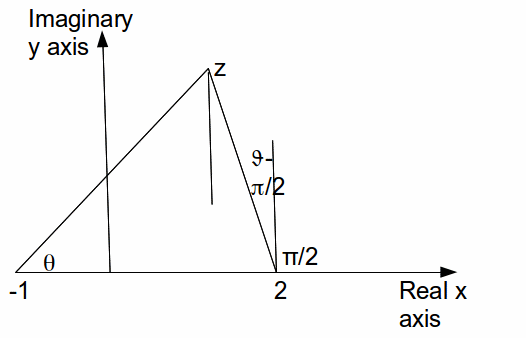
Fromdrop a vertical and label the angles formed as below.

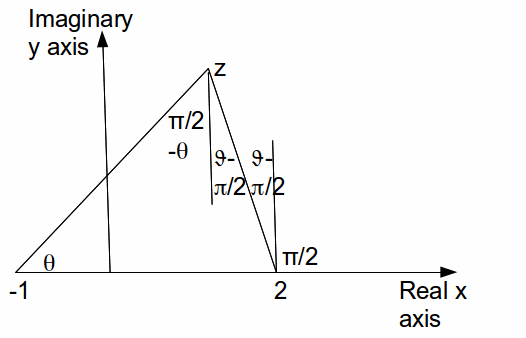
Atthe two anglesandadd to give angleswhich equalsfrom the original condition. This means that the interval from -1 to 2 is the diameter of a circle andis on the circumference, since the angle subtended equalsThe centre of the circle isand the radius is 1.5. The equation of the circle is