When attempting to sketch curves of functions of quotients of linear factors, it is best to start by sketching the asymptotes, which imply the behaviour of the function as one coordinate tends to infinity.
If the denominator factorises or has real roots, then there is a vertical asymptote for each root![]() of the form
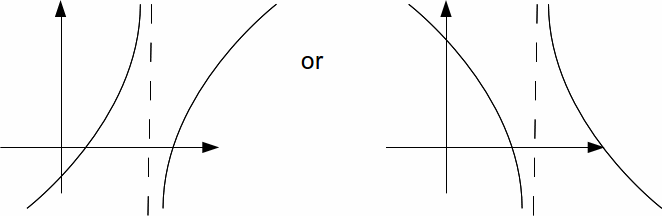
of the form![]() Each distinct linear factor gives rise to an asymptote such that the sign of the
Each distinct linear factor gives rise to an asymptote such that the sign of the![]() becomes
becomes![]() or vice versa as the asymptote is crossed.
or vice versa as the asymptote is crossed.
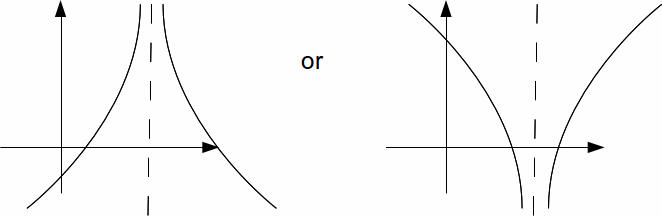
If a linear factor is squared the![]() does not change sign.
does not change sign.
We can find![]() – asymptotes by letting
– asymptotes by letting![]() tend to infinity and manipulating the numerator to allow terms to cancel if possible.
tend to infinity and manipulating the numerator to allow terms to cancel if possible.
If the degree of the denominator is greater than the degree of the numerator the y – asymptote is![]() For example
For example![]() has a
has a![]() – asymptote
– asymptote![]() because the degree of the numerator is 1 and the degree of the denominator is 2.
because the degree of the numerator is 1 and the degree of the denominator is 2.
If the degree of the denominator equals the degree of the numerator then the![]() – asymptote equals the quotient of the coefficient of the highest powers of
– asymptote equals the quotient of the coefficient of the highest powers of![]() For example
For example![]() has a
has a![]() – asymptote
– asymptote![]() because the degree of the numerator equals the degree of the denominator (both equal 2) and the coefficient of
because the degree of the numerator equals the degree of the denominator (both equal 2) and the coefficient of![]() in the numerator is 3 and the coefficient of
in the numerator is 3 and the coefficient of![]() in the denominator is 2.
in the denominator is 2.
We can also find intersections with axes if these exist by setting![]() and
and![]() respectively. If
respectively. If![]() putting
putting![]() gives the intersection with the
gives the intersection with the![]() – axis as
– axis as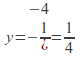 and putting y=0 implies
and putting y=0 implies![]()
