Group Generators

For each cyclic groupthere is an element – not necessarily unique – that generates the group, so that every element of the group is a result of repeated composition of some element with itself. Ifis such an element, and the grouphaselements, we can write

A group does not have to be cyclic to have a set of elements that generate the group. The group of symmetries of the rectangle is generated by the elementsandreflections in the vertical and norizontal lines through the centre of the rectangle.

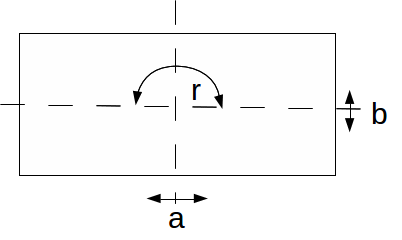
The group of symmetries isHoweveandsois said to generate the group. Other choices are possible.andalso generate the group.

Similary the group of symmetries of the equliateral triangle,is generated by the setsinceandOther choices are possible.andalso generate the group.andalso obey the relationship

Knowing the generators of as group and the relationships between them allows us to simplify any expression involving the elements of the group.

For the groupabove, suppose we have the sequence of operation on the equilateral triangle(1).

impliesso

(1) becomes

then implies

Finally,