A second order constant coefficient linear differential equation is any equation of the form
where
and
are constants. Solving these involves
Finding a solution
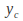of the homogeneous equation
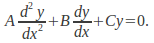We may assume a solution of the form
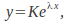obtaining the 'characteristic' equation
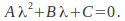If this equation has two distinct real roots
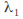and
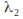then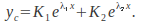
If the equation has a single repeated root
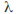then
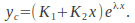If the equation has complex roots
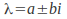then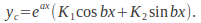
Now find a particular solution
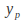of the inhomogeneous equation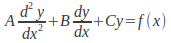by assuming a solution similar to the function
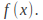For example if
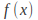is a polynomial of degree
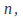then assume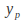is also a polynomial of degree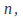so that if
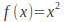then assume
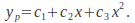The constants
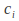can be found by equating coefficients.The general solution is the sum of the complementary and particular solutions:
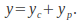The constants
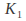and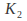
can be found if we are given two conditions on
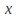and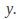
Example: Solve the equation
if
and
at
Assuming a solution to the homogeneous equation
of the form
we have
and
The equation becomes
The complementary solution is then
Assume a particular solution of the form
and
so the equation becomes
Equation coefficients ofgives
Equating constants gives
The particular solution is then
We have
The first conditiongives
The second condition gives
The solution to the problem is