Finding the Vector Equation of a Line Using the Cross Product

A line can be defined in terms of the cross product using the fact that ifis the position vector of a particular fixed point on the line relative to the origin andis the position vector of a general point on the line, thenis parallel to the line, or more precisely, the tangent vector of the line. This means that(1) whereis the tangent vector along the line sine the cross product of parallel vectors is zero.

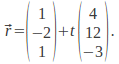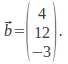We can use this to find the vector equation of a line. Suppose we have the line given by vector equationTakeThe tangent vectorWith we have

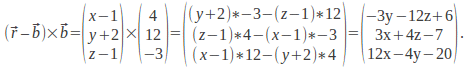
To show this gives the same line as the vector equation for the line, we can put

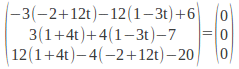as required by (1).