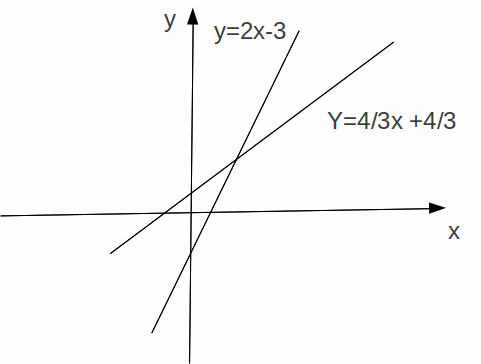Any transformation
represented by a matrix
whose entries are numbers is linear. The matrix will send a line to a line. The transformed line will in general be rotated and scaled, but it will still be a line. For example, suppose a transformationis represented by the matrix
Consider the effect ofon the line
The line may be represented by the vector
sends
to
Hence
and
Rearranging the first of these gives
Substitute this into the second to obtain
The labels
and
are arbitrary, so we can write
The property of the transformation that sends a line to a line is a reflection of the fact that the entries in the matrix are constants, so the thatandare linear functions of
can then be eliminated betweenandby simple substitution. The original and transformed lines are shown below
