The matrix representing a general rotation in three dimensions is
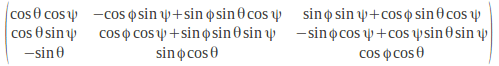
This is a complicated matrix but for rotations about one of the coordinate axes it simplifies considerably.
A rotation about the![]() - axis fixes
- axis fixes![]() We need a 1 in the top left hand corner and zero's in the first row and column. Take
We need a 1 in the top left hand corner and zero's in the first row and column. Take![]() to give.
to give.
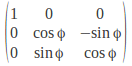
A rotation about the![]() - axis fixes
- axis fixes![]() We need a 1 in the middle and zeros in the second column and row. Take
We need a 1 in the middle and zeros in the second column and row. Take![]() to give
to give
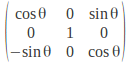
A rotation about the![]() – axis fixes
– axis fixes![]() We need a 1 in the bottom right hand corner and zeros in the third column and row. Take
We need a 1 in the bottom right hand corner and zeros in the third column and row. Take![]() to give
to give
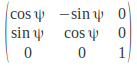
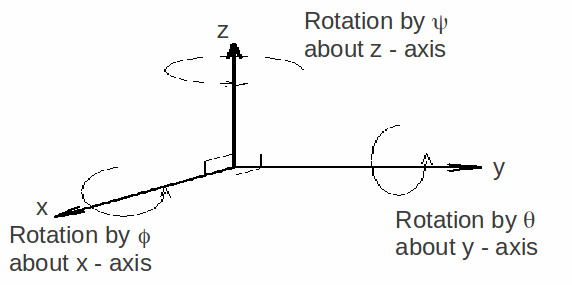
The angles![]() are called Euler angles. The general rotation matrix can be obtained by multiplying the three rotation matrices together.
are called Euler angles. The general rotation matrix can be obtained by multiplying the three rotation matrices together.
