More Advanced Projectile Questions

Advanced questions involving projectiles typically involve both horizontal and vertical components of motion. We use the equations of motion vertically and horizontally to find missing values ofandIn general values ofandare different considered horizontally and vertically, but the timeis the same at any instant of vertical or horizontal motion. In addition

1. The horizontal component of acceleration is zero so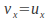at every point.

2. The vertical acceleration is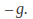The negative sign indicates the acceleration is always directed downwards, and is consistent with the sign convention taking upwards as positive and downwards as negative.

3. At the highest point, the vertical component of velocity is zero.

For example, suppose a ball is thrown horizontally from a window 6m above the ground. It just passes over a wall a horizontal distance 3m from the wind and hits the ground 4m behind it. We may draw a diagram:

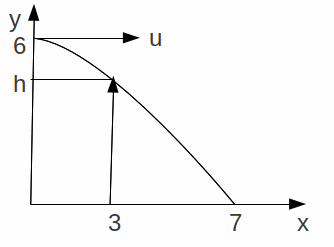
We want to find the speedand the height of the wall.

We can draw up the following table for the entire motion, up until when the ball hits the ground.

We can calculate the time taken for the ball to hit the ground by considering the vertical motion.

We put this into the table in both columns, because time is the same vertically and horizontally.

Now we can findby considering the horizontal motion.

The time to reach the wall can now be found by considering the horizontal motion.

Again write this time in both vertical and horizontal columns.

Work out the vertical distance fallen before passing over the wall using

Hence the height of the wall is