A framework is a connected network of rods. Each rod is assumed to be weightless, inflexible or rigid and inextensible, with thickness of zero. We typically want to find the forces in each rod, and these assumptions means the equations we write down are easy to solve.
Assuming the rod is weightless means the only forces acting are external to the framework. Generally these are known
If the rods are inflexible and rigid, then they cannot bend or stretch. If they bent or stretched then angles at points where the rods are joined to each other would also have to be calculated,
If the rods were not inextensible then their lengths would not be constant and would also have to be calculated.
If the rods had thickness, they taking moments about a point would be much more complicated because we should have to take into account the distance from any point of contact to the centre of the cross sectional area of the rod (assuming the rod is uniform).
The simplest framework is shown below, consisting of three rods of equal length 1m. It is supported at A and B, and a weight of 50N is hung from the top of the framework, point C. Find the reactions at A and B.
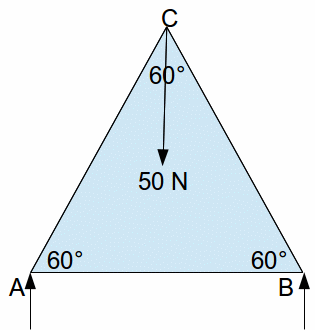
There are tensions in each rod. Assume that each rod is in compression so that the forces act outwards from the centre of each rod.
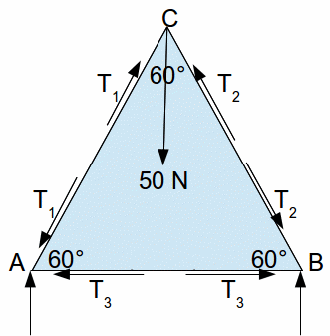
Since the framework is in equilibrium, the horizontal forces at each point balance, and the vertical forces at each point balance/
Equating forces at C gives
Equating forces at C gives
From these two equations
and
Resolving horizontally at A gives
Equating forces vertically at A gives
Resolving vertically at B similarly gives