The distance in four dimensional spacetime between two events with coordinates
and
according to one inertial observer O is
and to another inertial observer O' who observes the two events to have coordinatess
and
is
so that both observers obtain the same value
We can write these expressions as generalized dot products.
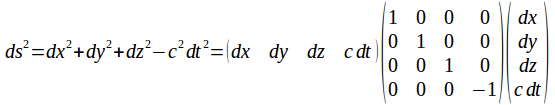
The transformation from
to
is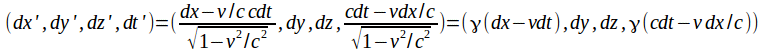
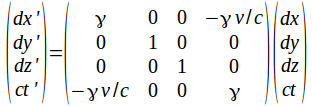
The determinant of the transformation matrix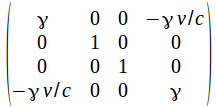
by expanding along the top row is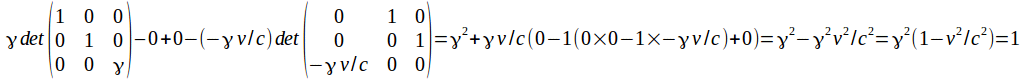
The dot product defined above preserves distances under the Lorentz transformation. Any vector satisfying the distance preserving property is called a 4 – vector. Examples are momentum and energy
and electric/magnetic fields or current and charge density.