A moving particle general has two sorts of energy – kinetic and potential. If conservation of energy can be applied to the particle – if no or other external forces eg friction acts – then the total energy will remain constant.
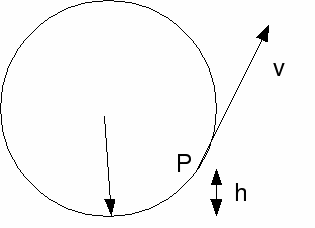
Motion in a circle is a special case. There is an external force – the tension in the string that keeps the particle moving in a circle, but the particle never actually moves in the direction of the force. At any time the particle is moving tangentially to the circle and the force is directed towards the centre of the circle – along it's radius. Tangent and radius being at right angles, the particle never moves in the direction of the force. This means that the force never does work on the particle, and the energy of the particle is conserved, if we ignore friction.
Kinetic Energy + Gravitational Potential Energy=Constant.
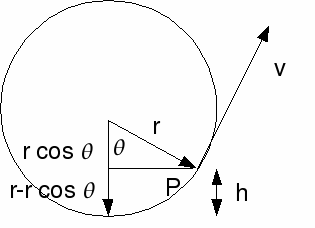
If we take the bottom of the circle as the zero of potential energy then
and
(1)
At any point on the circle as the particle moves we can apply F=ma towards the centre of the circle.
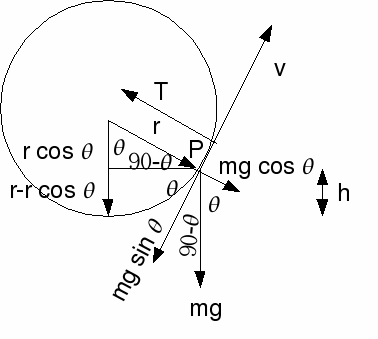
(2)
From (1)
Sub this into (2)
Taking the centre of the circle as the zero of potential energy gives
is usually calculated out from the initial conditions.