The moment of Inertia of a body about a point, labelled
is found by summing or integrating the moments of inertia of the particles that constitute the body:
for a collection of discrete particles with masses
at positions
where
with
equal to the mass of the small region
of density
where
is the mass of the body at the point and the integral is carried out over the space
(which may be a line, area or volume) occupied by the body
For example, the moment of inertia of a circular piece of card of uniform mass per unit area and radius
about an axis perpendicular to the card passing through the centre can be found by integration.
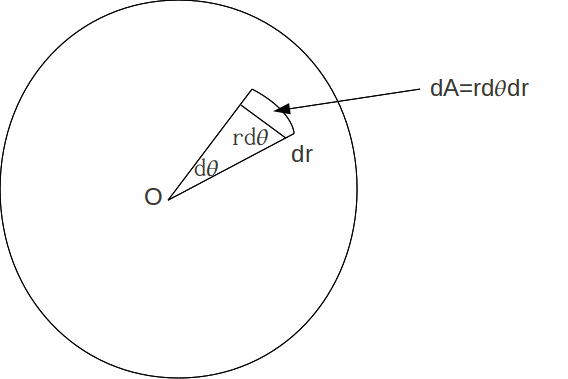
From the diagram above,
so
hence
The mass of the card is
so