\[u \mathbf{j}\]
m/s on level ground and finds the apparent velocity of the wind is \[v(3 \mathbf{i} - 4 \mathbf{j} )\]
m/s.When he cycles with velocity
\[ \frac{u}{5}(-3 \mathbf{i} + 4 \mathbf{j} )\]
m/s, the apparent velocity of the wind is \[w \mathbf{i}\]
m/s.What is the true wind velocity?
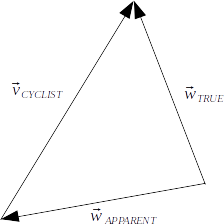
The diagram below illustrates that the true wind speed is
\[\mathbf{w}_{TRUE}=\mathbf{v}_{CYCLIST}+ \mathbf{w}_{APPARENT}\]
.
\[\mathbf{w}_{TRUE}=u \mathbf{j}+v(3 \mathbf{i} - 4 \mathbf{j} )=3 v \mathbf{i} +(u- 4v) \mathbf{j}\]
\[\mathbf{w}_{TRUE}=\frac{v}{5}(-3 \mathbf{i} + 4 \mathbf{j} )+w \mathbf{i}=(- \frac{3v}{5}+w) \mathbf{i} - \frac{4v}{5} \mathbf{j}\]
Equating these
\[3 v \mathbf{i} +(u- 4v) \mathbf{j}=(- \frac{3v}{5}+w) \mathbf{i} - \frac{4v}{5} \mathbf{j}\]
Equating components:
\[3 v=(- \frac{3v}{5}+w)\]
(1)\[u- 4v = - \frac{4v}{5}v \]
(2)From (1)
\[3.6 v=w\]
and from (2) \[u=4.8v\]
so \[w=\frac{3.6}{4.8}u=\frac{3}{4}u\]
.\[\mathbf{w}_{TRUE}=(- \frac{3v}{5}+w) \mathbf{i} - \frac{4v}{5} \mathbf{j}=(- \frac{3u/4.8}{5}+\frac{3}{4}u) \mathbf{i} - \frac{4u/4.8}{5} \mathbf{j}=- \frac{u}{6} \mathbf{j}\]
Equating these
