If we rotate a body about an axis, we will be increasing its angular momentum. The moment of inertia I of a body is a measure of its resistance to increasing angular momentum. If the body is just a single point particle of mass m, a distance r from the axis then
In general a body is extended in space and has a continuous mass distribution. We must use integration to find the moment of inertia using the formula
For example to find the moment of inertia of the uniform lamina illustrated below.
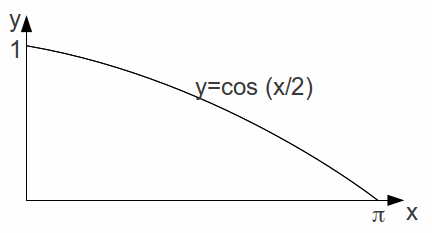
About the
axis the moment of inertia is
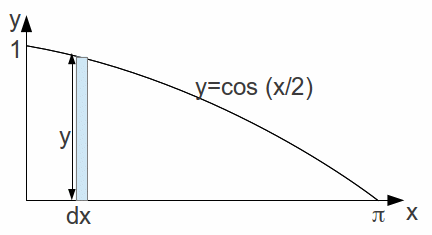
by breaking the area into vertical strips and the limits of integration are then
About the
axis the moment of inertia is
as before by breaking the area into vertical strips and the limits of integration are still
