Modelling the Motion of Raindrops - Mass increasing at Rate Proportional to mv

As raindrops fall, they tend to grow. If a raindrop of massis falling through a stationary cloud, then for each infinitesimally small amount that the raindrop grows by, momentum is conserved at the instant of growth. At the same time, gravity is pulling the raindrop down with a force Suppose the raindrop is accumulating mass at a ratewhereis a constant andis the speed of the raindrop. If during a timethe momentum of the raindrop increases by

then assumingis constant during the time interval

Dividing bygives

Now letto give the differential equation

If the mass of the raindrop is increasing at the ratethenso

WriteThe equation becomes

Separating variables gives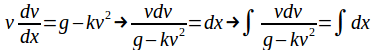

On integrating we obtain

If v=0 when
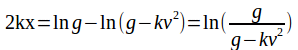
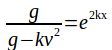