If we have three objects, labelled A, B and C, there are six distinct ways thes objects can be arranged in a line:
ABC, ACB, BAC, BCA, CAB and CBA
If these objects are arranged in a circle, we may be only interested in their relative seating positions, which is next to/to the left of/to the right of some other one.
If the direction in which we are moving around the table matters, there are only two distinct arrangements,
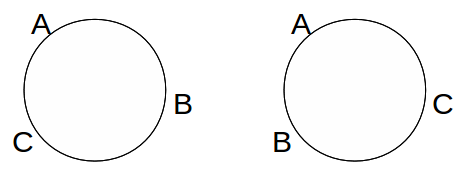
since in the following seating arrangements, the relative position of each is the same with respect to the others.

If orientation does not matter, then there is only one distinct seating arrangement. A is always postioned between B and C. B is always positioned between A and C, and C is always positioned between A and B.
We could analyse with factorials and![]() and
and![]() notation.
notation.
There are 3! possible arrangements with respect to position, but since each may sit in one of 3 places,![]() relative seating arrangements with respect to orientation, and since any two can interchange without changing what object is next to another, there are
relative seating arrangements with respect to orientation, and since any two can interchange without changing what object is next to another, there are![]() arrangements with respect to relative position without orientation.
arrangements with respect to relative position without orientation.
We can generalise this to more objects arranged in a circle. If![]() objects are arranged in a circle, there are
objects are arranged in a circle, there are![]() arrangements with respect to relative position and
arrangements with respect to relative position and![]() arrangements with respect to relative position without orientation.
arrangements with respect to relative position without orientation.
