The normal distribution is the most useful and widely usedstatistical distribution, but it can't be used everywhere. Whenconsidering whether or not a distribution can be modelled by thenormal distribution we should keep in mind the main features of thenormal distribution:
It is a bell shaped curve symmetrical about the mean. It has noskew.
It is very unlikely, though possible, that values occur which areless or more than three standard deviations from the mean.
There are no upper or lower cut off points. In theory a randomvariable which has a normal distribution may take any values from![]() to
to![]()
Of course, if we take a random sample of some variable we wouldnot expect the random sample to be exactly randomly distributed, norexactly bell shaped and maybe there are some quite extreme valueswell below or above three standard deviations from the mean, but ifthe conditions are 'approximately' met or a histogram of values is'not too far' from that we would expect from a normal distributionthen we can often take the normal distribution to be suitable.
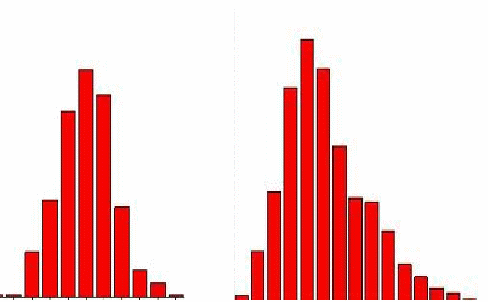
The histogram on the left indicates a normal distribution isplausible. The histogram on the right indicates positive skew so anormal distribution is unlikely to be unsuitable.
We may be able to reject a normal distribution as suitable ontheoretical grounds if the set of possible values is limited in someway. Heights and weights may not take values less than zero so intheory these can not be modelled by a normal distribution, though infact they often are.
