A statistic is a single measure of some attribute of a sample e.g.the mean. It is calculated by applying a function to the set of data.
More formally, statistical theory defines a statistic as afunction of a sample where the function itself is independent of thesample's distribution; that is, the function can be stated before thedata is taken. The term statistic is used both for the function andfor the value of the function on a given sample.
A statistic is distinct from a statistical parameter – the meanor standard deviation for example - which is not computable becauseoften the population is much too large to examine and measure all itsitems, or because the population is transitory – for example tofind the average age of the UK population, you could find the mean ofthe whole population, but people are dying and being born all thetime, so the average age is not a constant number but is itselffluctuating. The average age just described is in fact a randomvariable.
A statistic, when used to estimate a population parameter, iscalled an estimator. For instance, the sample mean is a statisticwhich estimates the population mean, which is a parameter. Inpractice, all parameters are estimated by some statistic. Estimatorsof parameters are often denoted with a hat, so an estimator of
maybe written
Example: Suppose we have a sample of observations
We can find an estimate of the mean
Thisis a statistic because it is computed from the data, even though notall the data are used.
Example: Using the same sample above, we can find an estimator forthe variance.
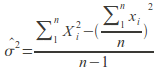
The function above is a statistic because it is calculated usingonly the data, but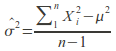
is not a statistic because it is calculated using theparameter
whichis not calculated from the data.