If a probability distribution is such that any valu ebetween two limits
is equally likely then the uniform distribution,
may be suitable. The Uniform distribution may be either continuous eg sometime in the next hour the postman will arrive, or discrete eg the score on a fair dice.
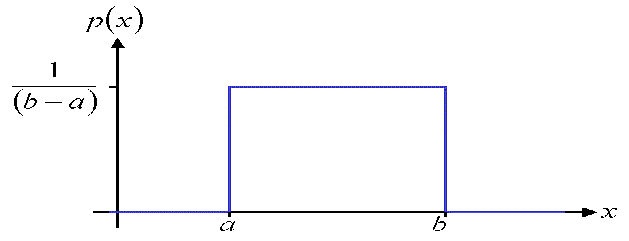
The mean of the Uniform distribution is the midpoint ofthe interval
where the distribution is discrete or continuous is
thevariance
and the probability density function
(for a continuous distribution) or probability mass function
(for a discrete distribution with n possible outcomes) and cumulative distribution function 
whether the distribution is discrete or continuous. The cumulative distribution function is for both continuous and discrete distributions If the distribution is continuous then neither, one or both endpoints may be possible values for the random variable, but if the distribution is discrete then both endpoints MUST be possible values for the random variable.
Example: The lengths of snails are uniformly distributed over the interval
with the lengths of snails independent of each other. Find the probability that two snails both have lengths less than 1.4.
Since the lengths of the snails are independent of each other,