Formulating Null and Alternative Hypotheses

Every hypothesis test seeks to prove or disprove astatistical statement about a population to a particular level ofcertainty. In order to do this the statement needs to be clearlyphrased.

Typically the statement is about the mean of adistribution or the probability of an event occurring. The nullhypothesis is the value that we suppose this mean or probability hasfor a certain probability distribution. This can be because, forexample:

1. The mean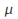(orprobability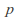)has had this value,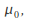(or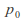)for a while, and we want to see if the latest set of data indicatesa change. In this case, our null hypothesis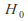wouldbe that the mean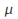(orprobability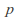)has this longstanding value and the alternative hypothesis is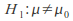(or).

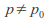2. That some manufacturer has made a claim about thesuperiority of his product over the product of some othermanufacturer. He might claim that 80% of cats prefer the 'Catlove'brand of catfood, manufactured by his company. In this case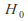couldbe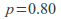andthe alternative hypothesis could be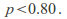

When the null and alternative hypotheses are drawn up,there is often a claim that is to be tested. In the first claimabove, there is no claim of increase of the mean, so the hypothesistest is conducted merely in order to see if there is evidence thatthe mean (or probability) has changed, not specifically increased ordecreased. Of course, in order to change, the mean (or probability)must either increase or decrease, but the assumption is not part ofthe test. In the second example above, the manufacturer of cat foodis making a suspect claim about the love of cats for his company'sbrand of cat food, and it must be suspected that in fact less than80% of cats prefer his company's brand. In this case therefore, asstated above, the null hypothesis would be that