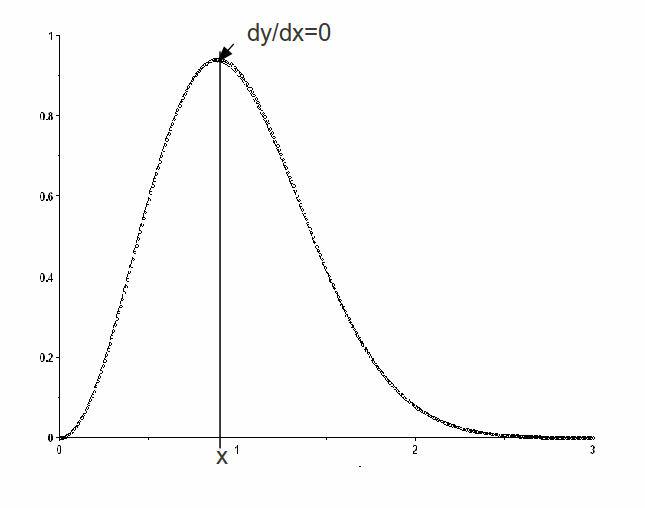
The mode of a continuous distribution is the most probable valueof the random variable associated with the distribution. If we sketchthe probability distribution function against
itwill typically have a maximum. Finding the mode then becomes a matterof finding the turning point, or solving the equation
Example: Find the mean of the probability given by
The Uniform distribution does not have a mode since
everywhere,except at the ends. Also if
isincreasing then the mode is at the upper end of the range of
andifisdecreasing then the mode is at the lower range of the distributionof