Sampling Distribution of the Mean of a Sample - The Central Limit Theorem

Supposeis a random variable from a population with meanand standard deviation

Supposeis a random sample of size n with mean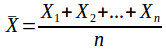then the expected mean of the population of sample means is

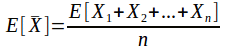
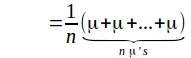
The expected variance of the population of sample means is

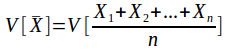
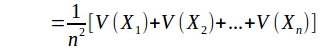
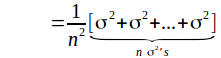
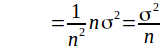
If very many samples were taken and the mean of each sample calculated then the mean of these means would beand the variance of these means would be

It can also be shown that the sample means form a Normal distribution (provided that n is ‘large

enough’). This is the 'Central Limit Theorem'.

We can then say that for samples of sizedrawn from a population with meanand variancethe sampling distribution of the sample means is