The Goodness of Fit or Chi - Squared Distribution

Thetest can only be used the goodness of fit of a data set to a hypothesised probability distribution.

The observed data is sorted into frequency classes, and for each frequency class, the expected number of observations that would fall into that frequency class is calculated.

The difference between each observed frequency O-i and expected frequency E-i is calculated, squared and divided by the expected frequency. This calculation is performed for each frequency class and the results are all added to give a single number, the test statistic, equal to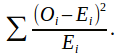

If the expected frequency for a frequency class is less than 5,then this group is combined with other frequency classes so that all frequency classes have expected frequencies at least equal to 5.

The significance of the test statistic depends on the number of degrees of freedom,of the data, which is equal to the number of frequency classes AFTER any classes have been combined, c, minus 1, so that

the test statistic is then compared with thevalue drawn from thetables, whereis some set level, to draw some conclusion.

Example:

A die is rolled 600 times and the frequency of each score recorded.

Test whether the die is fair at the 1% level of significance.

First state the null and alternative hypotheses,andrespectively.

The probability of each score is 1/6.

The die is not fair and the probability of each score is not 1/6.

The expected frequencies are all 1/6 × 600 = 50 so the test statistic is

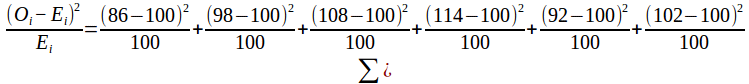
since the total is a linear equation connecting the frequencies and is fixed.

From tables we see thatso our result is not significant.

We do not rejectand conclude that the die is not unfair.