To test for the equality of the mean of a population, we can usethe central limit theorem, which states that the mean of a sample ofsize n from any population is approximately normally distributed,with the accuracy of the approximation improving with increasing n.When the variance of the population,
isnot known and the sample is large, we assume that the variance ofthe sample,
-the unbiased estimate of the population variance,
-is equal to
Calculations can then be done using the normal distribution.
Example: A machine is calibrated to produce nails with a meanlength of 5.4 cm. 80 nails are to be tested to ensure the machine isstill calibrated correctly. The sample has mean 5.31 cm and variance
so
Conducta hypothesis test at the 5% level of significance, to test whetherthe machine is calibrated correctly.
Solution:
The null and alternative hypotheses are respectively,
Using the central limit theorem, we assume
The test statistice is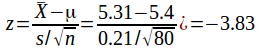
The hypothesis test is two tailed, so the area of each tail is0.025 or 2.5 %.
The critical values of z, corresponding to probability of 2.5%,are
sothe null hypothesis is rejected. There is evidence that the meanlength of the nail;s is not 5.4 cm. The machine needs to berecalibrated.