The paired t test is typically used to analyse whether there is a before and after difference. It is the same population before and after, and the difference for each individual is measured and a mean difference found and analysed for significance. For example:
Do patients with high blood pressure see a fall in drug pressure after taking a drug?
Do people earn more after getting a qualification?
Do people watch more TV after getting satellite TV?
For example suppose people with raised blood pressure are given a new drug which it is supposed reduces blood pressure. To test this, people are put on a two week course of drugs and their blood pressures are compared before and after. The results are illustrated in the following table.
|
Person |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
Before |
164 |
122 |
166 |
162 |
152 |
114 |
136 |
142 |
154 |
190 |
|
After |
150 |
120 |
148 |
137 |
152 |
122 |
132 |
138 |
142 |
170 |
|
Difference |
-14 |
-2 |
-18 |
-25 |
0 |
8 |
-4 |
-4 |
-12 |
-20 |
Suppose to test mean difference,
(there is no difference in blood pressure before and after taking the drug)we carry out a hypothesis test at the 10% level.
The null hypothesis is
The alternative hypothesis is
This is a two tailed test so we look in the statistical tables for
with10-1=9 degrees of freedom ie
The mean difference,
We calculate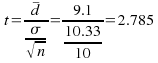
2.785 >1.833 so we reject
The drug does lower blood pressure.