A conical pendulum can be made to rotate in a circle with a constant radius while varying its length.
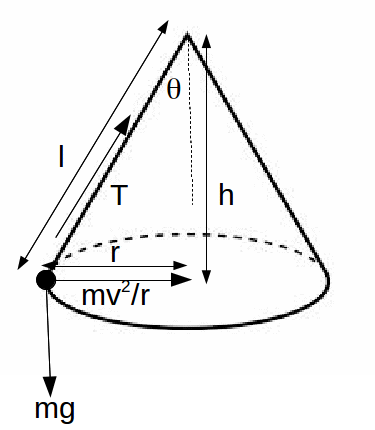
The diagram shows a conical pendulum of mass m rotating in a circle of radius r. The centripetal force making the pendulum rotate in a circle is equal to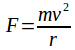 and is due to the horizontal component of the tension in the string.
and is due to the horizontal component of the tension in the string.
Resolving vertically for the pendulum of mass![]() gives
gives
![]() (1)
(1)
Resolving horizontally for the pendulum of mass![]() gives
gives
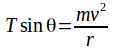 (2)
(2)
Dividing (2) by (1) gives
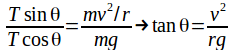
From the diagram above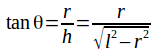
Hence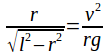
But![]() (the circumference of the orbit divided by the period) so
(the circumference of the orbit divided by the period) so
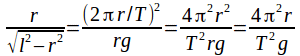
Cancelling r from both sides and inverting gives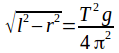
A graph of![]() on the y axis against
on the y axis against![]() on the x axis will have gradient
on the x axis will have gradient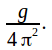
![]() is then equal to
is then equal to![]()
