Two equal and oppositely directed parallel but not collinear forces acting upon a body. The moment of the couple (or torque) is given by the product of one of the forces by the perpendicular distance between them:![]() in the diagram below.
in the diagram below.
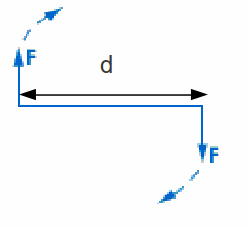
The moment of a force![]() is only defined with respect to a certain point P – the moment of
is only defined with respect to a certain point P – the moment of![]() about P - and in general when P is changed, the moment changes. However, the moment (torque) of a couple is independent of the reference point P : Any point will give the same moment. In other words, a torque vector, unlike any other moment vector, is a "free vector".
about P - and in general when P is changed, the moment changes. However, the moment (torque) of a couple is independent of the reference point P : Any point will give the same moment. In other words, a torque vector, unlike any other moment vector, is a "free vector".
Proof: Suppose there are a set of force vectors![]() etc. that form a couple, with position vectors (about some origin P )
etc. that form a couple, with position vectors (about some origin P )![]() etc., respectively. The moment about P is
etc., respectively. The moment about P is
Now we pick a new reference point P' that differs from P by the vector r . The new moment is
We can simplify this as follows:
![]()
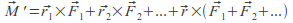
- The definition of a force couple means that
-
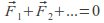
Therefore,
This proves that the moment is independent of reference point, which is proof that a couple is a free vector.
