Suppose a plane can fly at 650 km/h in still air. The wind is blowing at 80 km/h on a bearing of 0110 degrees. The pilot wants to flu North. He has to fly into the wind slightly as shown.
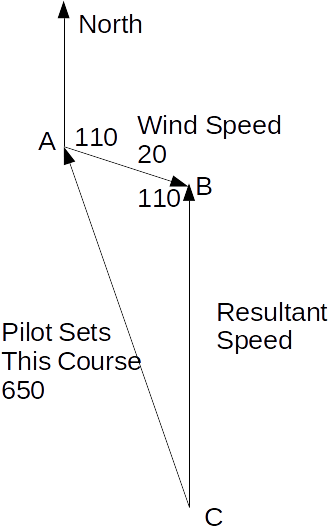
\[\frac{20}{sin C} = \frac{650}{sin 110} \rightarrow sin C =\frac{20 \times sin 110}{650} = 0.02891 \rightarrow C = 1.657\]
degree.Then
\[A=180-110-1.6576=68.343\]
degrees.Now use the Cosine Rule
\[a^2 =b^2 +c^2-2bc cos A\]
to get BC.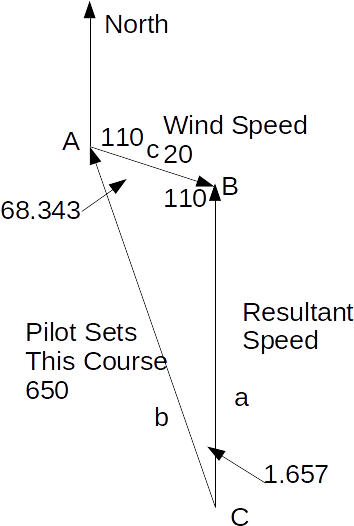
\[a^2 = 20^2 + 650^2 -2 \times 20 \times 650 cos 68.343 =423306 \rightarrow a=642.89\]
The pilot must steer into the wind at an angle 1,656 degrees Eat of North, and the plane will travel over the Earths surface at a speed of 642.86 km/h.
