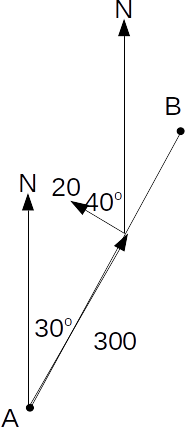
If the pilot aims the plane on to fly to B, he will be blow off course by the wind. What will be the ground speed and the bearing actually flown by the plane?
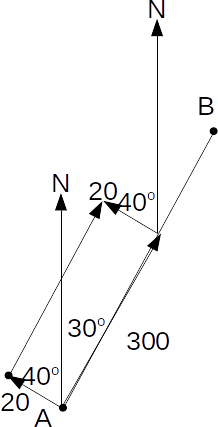
We can draw the vector diagram shown.
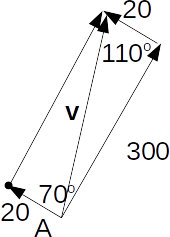
\[v=\sqrt{300^2+20^2-2 \times 300 \times 20 \times cos 110^o}=307.4 km/h\]
To find the bearing, we find the angle
\[x\]
below using the Sine Rule.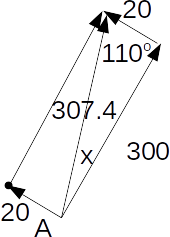
\[\frac{sinx}{20}=\frac{sin110}{300} \rightarrow x=sin^{-1}(20 \times \frac{sin110}{300} )=3.6^o\]
to 1 decimal place. The pilot will actually fly on a bearing of
\[30^o-3.6^o=26.4^o\]
to 1 decimal place.
