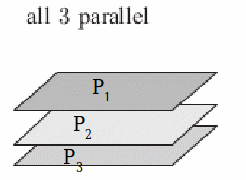
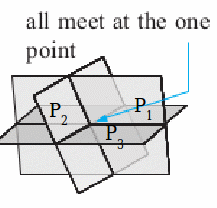
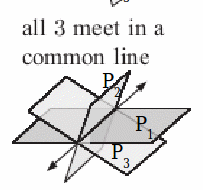
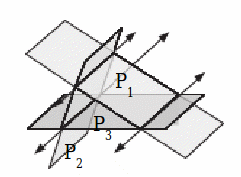
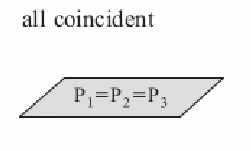Whether or not three planes intersect in points, lines or coincide depends on the relationships between the equations of the planes
| The equations of the planes are multiples of each other. For example
The second and third equations are double and triple the first respectively. |
| The equations of two planes are multiples of each other and the third is some other. For example
The second is twice the first. |
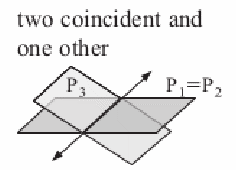
| Two of the planes are multiples of each other and but the third is not because the number on the right hand side fails.
|
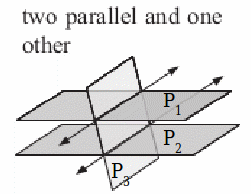
| Twow of the planes are parallel so the coeeficients are the same or multiples of each other and the third is not.
|
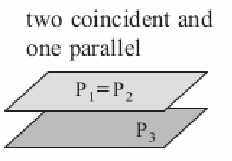
| All planes are parallel so the coefficients are multiples of each other but not the right hand side.
|
| All the equations are completely independent of each other.
|
| The equations are linearly dependent, so each equation can be written in terms of each other.
The first equation minus the second equation equations the third equation |
| Each pair of planes intesects and the line of intersection is parallel to the third plane. There is no common point of intersection.
The second equation minus 3 times the first gives The equations are inconsistent. |
and the third minus the first gives