\[\mathbf{a}, \; \mathbf{b}. \; \mathbf{c}\]
as shown.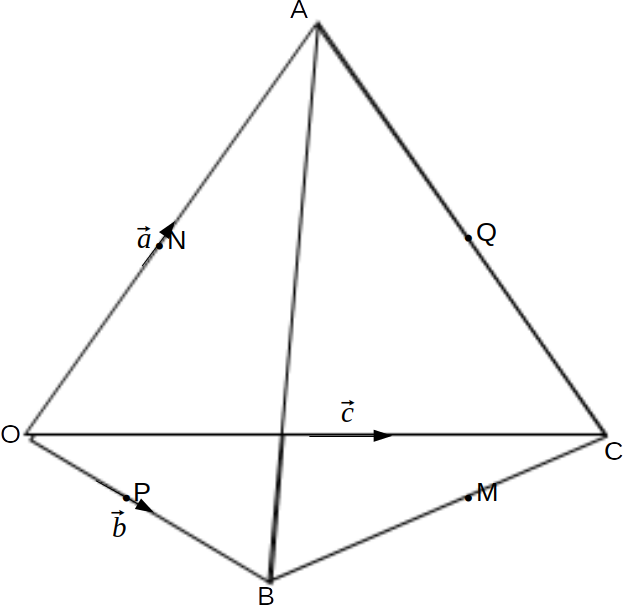
\[\mathbf{r}_{PQ}(t)=\frac{1}{2} \mathbf{b}+t(\frac{1}{2} \mathbf{b} - \mathbf{b}+ \mathbf{c} + \frac{1}{2} ( - \mathbf{c} + \mathbf{a})= \frac{1}{2} \mathbf{b} + \frac{t}{2} (\mathbf{a} - \mathbf{b}+ \mathbf{c})\]
M is the midpoint of the line BC and N is the midpoint of the line OA. The equation of the line MN is
\[\mathbf{r}_{MN}(s)=\mathbf{b}+ {1}{2} (- \mathbf{b} + \mathbf{c} ) + s(-\frac{1}{2}(- \mathbf{b} + \mathbf{c} )- \mathbf{b} + \mathbf{a})= \frac{1}{2} (\mathbf{b} + \mathbf{c})+ \frac{s}{2} (\mathbf{a} - \mathbf{b}- \mathbf{c})\]
Equate the coefficients of
\[\mathbf{a}, \; \mathbf{b}, \; \mathbf{c}\]
:\[\mathbf{a}\]
: \[\frac{t}{2}= \frac{s}{2} \rightarrow t=s\]
\[\mathbf{b}\]
: \[\frac{1}{2}- \frac{t}{2}= \frac{1}{2}- \frac{s}{2} \rightarrow t=s\]
\[\mathbf{c}\]
: \[ \frac{t}{2}= \frac{1}{2}- \frac{s}{2} \rightarrow t=s= \frac{1}{2}\]
Hence by symmetry the lines bisect each other.
