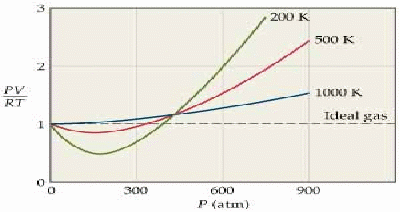
The ideal gas equation![]() is derived using a simple model of a gas that ignores the attractive forces between the gas molecules and their volume. The model becomes less satisfactory as the pressure increases and the molecules are forced closer together, and the temperature decreases, so the gas gets closer to condensing.
is derived using a simple model of a gas that ignores the attractive forces between the gas molecules and their volume. The model becomes less satisfactory as the pressure increases and the molecules are forced closer together, and the temperature decreases, so the gas gets closer to condensing.
We can make approximate corrections for these two factors by:
-
Taking the volume of the gas as the volume of the container minus the volume of the gas molecules, or a least minus a term that depends on the volume of the gas molecules. The volume becomes
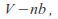 where
where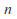 is the number of mols of gas and
is the number of mols of gas and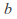 is a constant which depends on the gas in question.
is a constant which depends on the gas in question. -
Including a term added to the pressure to take account of the attractive force between the molecules. The attractive force between the molecules is proportion to the number of molecules per unit volume near the wall, and also in the interior of the gas so proportional to
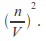 This means the effective pressure becomes
This means the effective pressure becomes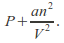
With these modifications the ideal gas equation becomes![]()
When![]() is small, so the gas is dilute, the average distance between gas molecules is large, so that
is small, so the gas is dilute, the average distance between gas molecules is large, so that![]() is small,
is small,![]() and the extra terms in the van der Waals equation become insignificant. As an example, for
and the extra terms in the van der Waals equation become insignificant. As an example, for![]() and
and![]() One mol of an ideal gas at a temperature of 0 degrees celsius and a pressure of 1 atmosphere or
One mol of an ideal gas at a temperature of 0 degrees celsius and a pressure of 1 atmosphere or![]() occupies a volume of
occupies a volume of![]() According to the van der Waals equation the same amount of gas at the same volume and temperature would exert a pressure only 532 Pa less, a difference of about 0.5%.
According to the van der Waals equation the same amount of gas at the same volume and temperature would exert a pressure only 532 Pa less, a difference of about 0.5%.
