Simple harmonic motion of a body is motion in a straight line about a point such that the acceleration of the body is always directed towards the equilibrium point, labelled O below, and the magnitude of the acceleration is proportional to the distance from the point. We may illustrate this in the diagram below, in which the double headed arrows indicate the acceleration.
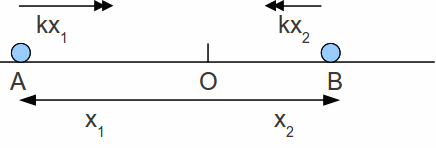
In the diagram above the body is moving backwards and forwards about the point O.
At A the distance of the body from O is
and the acceleration is
towards O.
At B the distance of the body from O is
and the acceleration is
towards O.
At the point A it does not matter whether the particle is moving away from O or towards O: the acceleration is stilltowards O. At the point B it does not matter whether the particle is moving away from O or towards O: the acceleration is still
towards O – the acceleration is always directed towards O. Mathematically we may write
This equation states that the acceleration is proportional to the displacement from the equilibrium point and directed opposite to the displacement.
Simple harmonic motion is naturally related to motion in a circle.
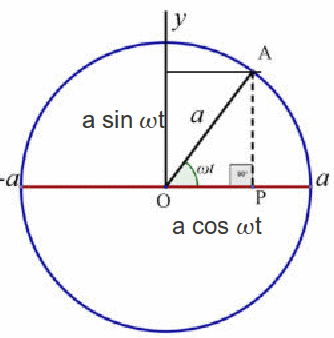
We can use simple trigonometry to project motion in a circle onto the
axis in the diagram above using simple trigonometry:
where
is the rate of change of the angle with theaxis, and is called the angular velocity.
If we differentiate this twice to get the acceleration, we obtain
Compare this with
to obtain