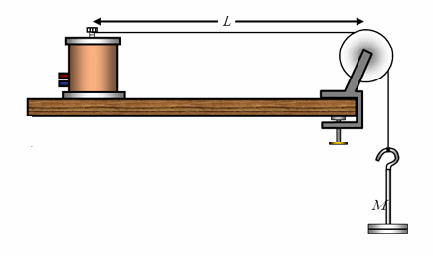
Standing waves may be produced using the apparatus above. The electromagnetic on the left vibrates up and down with the frequency of an applied alternating potential difference. These vibrations send waves along the string which are reflected at the pulley and arrive back at the electromagnet. The wave undergoes a phase change of
equivalent to half a wavelength, on reflection at each end. If when the vibration arrives back at the electromagnet, the magnet has gone through one complete cycle or vibration, the the wave which has been reflected will be in phase with the wave now being produced and there will be constructive interference. This will happen at a certain frequency of vibration, called the fundamental frequency, for the electromagnet. When this happens, for the sort of apparatus shown above, where one end is fixed and the other forced to vibrate, we have a standing wave, shown as the top picture below
If we increase the frequency, the standing wave is destroyed, but at a certain frequency we obtain a new standing waves with two antinodes. This it the second harmonic, or first overtone shown below. The frequency of this vibration is twice that of the fundamental, and the wavelength is halved. If we increase the frequency further we see that for each successive standing wave, the frequency increases in increments of the fundamental frequency.
In general the speed of the standing wave is constant - a property of the apparatus and not the frequency or wavelength. The frequency of the n th harmonic is nf and the wavelength of the n th harmonic is
