The diagram below shows two loudspeakers A and B a distance 0.8 m apart producing coherent sound of the same frequency and wavelength. 2 m away from the line joining the loudspeakers is parallel line along which a detector C is moved. When ABC form a right angle constructive interference occurs and the path difference between AC and BC is one wavelength.
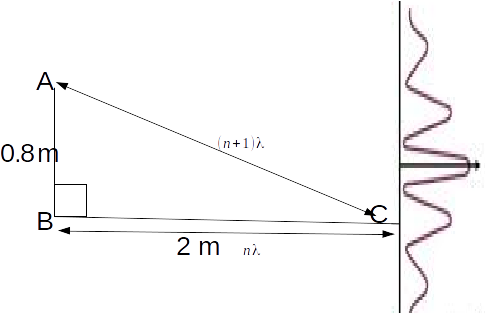
\[AC^2 =BC^2 +AB^2 =2^2 +0.8^2 =4.64 \rightarrow AC= \sqrt{4.64} = 2.1541 m\]
to four decimal places. The wavelength is
\[\lambda=2.1541-2=0.1541 m\]
.
