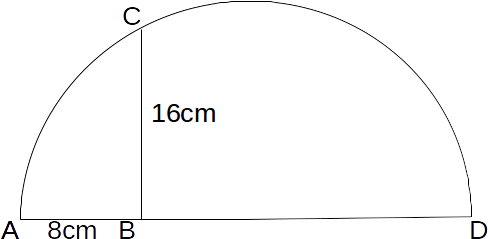
If
\[\angle BAC =x\]
then \[\angle BCA = 90-x\]
and \[\angle DCB=90-(90-x)=x, \: \angle BDC=90-x\]
.Triangles ABC and BDC have three identical angles, so are similar triangles.
Then
\[\frac{AB}{BC}=\frac{BC}{BD} \rightarrow BD=\frac{BC \times BC}{AB}=\frac{16^2}{8}=32\]
