\[y=f(x)\]
is translated by the vector \[\begin{pmatrix}1\\3\end{pmatrix}\]
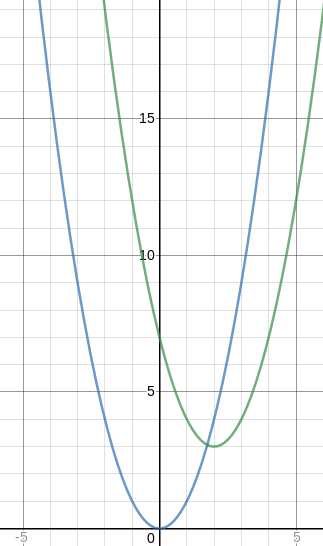
. What will the equation of the resulting graph?The vertex of the graph is initially at
\[(0,0)\]
and is moved to \[(1,2)\]
by the translation.
A translation of \[{} +2\]
in the \[x\]
direction results in the relabelling \[f(x) \rightarrow f(x-2)\]
so \[f(x)=x^2\]
becomes \[f(x-2)=(x-2)^2\]
and the translation of \[{} +3\]
in the \[y\]
direction results in the relabelling \[f(x) \rightarrow f(x)+2\]
.Hence the equation of the translated curve is
\[y=(x-2)^2+3=x^2-4x+4+3=x^2-4x+7\]
.