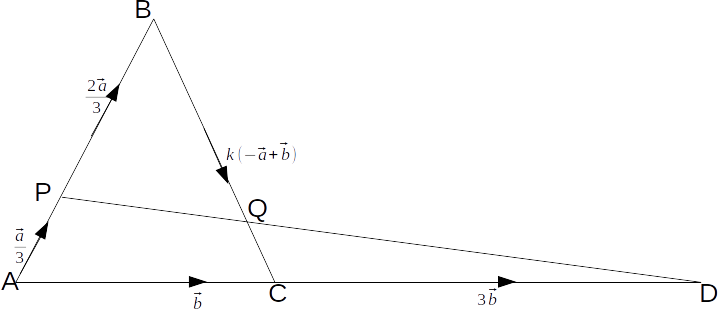
BQ=k(BC) and PQD is a straight line.
If
\[\mathbf{AB}=\mathbf{a}, \; \mathbf{AC}=\mathbf{c}, \; \mathbf{CD}=3\mathbf{a}\]
find the value of \[k\]
.Since P splits AB in the ratio 1:2,
\[\mathbf{AP}=\frac{1}{3} \mathbf{a}, \; \mathbf{PB}=\frac{2}{3} \mathbf{a}\]
.\[\mathbf{BC}=- \mathbf{a}+ \mathbf{b}\]
so \[\mathbf{BQ}=k(- \mathbf{a}+ \mathbf{b})\]
.
\[\mathbf{PQ}= \mathbf{PB}+ \mathbf{BQ} =\frac{2}{3} \mathbf{a}+k(- \mathbf{a}+ \mathbf{b})=(\frac{2}{3}-k) \mathbf{a} + k \mathbf{b}\]
\[\mathbf{PD}= - \frac{1}{3} \mathbf{a} ++4 \mathbf{b}\]
.\[PQD\]
is a straight line so \[\mathbf{PQ}, \; \mathbf{PD}\]
are parallel and the coefficients of \[\mathbf{a}, \; \mathbf{b}\]
are in the same ratio.Hence
\[\frac{2/3-k}{-1/3}= \frac{k}{4} \rightarrow\frac{8}{3}-4k=- \frac{k}{3} \rightarrow \frac{8}{3}= \frac{11k}{3} \rightarrow k =\frac{\frac{8}{3}}{\frac{11}{3}}=\frac{8}{11}\]
