When solving ordinary – linear –simultaneous equations we multiply the equations by constant factorsto make the coefficient of some variable the same in magnitude, thenadd or subtract the equations to eliminate that variable.
For example, solve
(1)
(2)
(1)*2-(2)*3 eliminates
togive
Substitution of this value ofinto(1) to find a gives
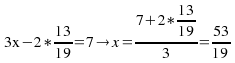
If one of the equations is a quadratic wemay not be easily able to rearrange the equations to easily eliminateone of the variables and solve the equations. But we can rearrangeone of the equations – usually the linear one - to makeeither
or
thesubject.
Example:
(1)
(2)
Rearrange (1) to makethesubject:
andsubstitute this into (2) to get
To solve the last equation we can eitherfactorise or use the quadratic formula.
By factorising:
or
If
from
If
from
By using the quadratic formula:
hence
or3.
As before , substitute these values of
backinto (1) to obtain