Displaying the number
\[z=x+ i y\]
(where \[x, \: y\]
are the real and imaginary components of \[z\]
respectively, and \[i=\sqrt{-1}\]
on an Argand diagram means plotting the point \[(x,y)\]
and drawing a line from the origin to the point.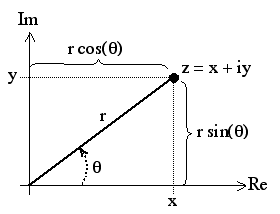
\[z\]
is the length of the line so \[|z|= \sqrt{x^2+y^2}\]
and the argument of \[z\]
, written \[Arg(z)\]
is the anfle \[\theta\]
that \[z\]
makes with the positive real (or \[x\]
) axis. takien counter clockwise.We can also write
\[z= x+iy = \sqrt{x^2+y^2} e^{i tan^{-1}(y/x)}\]
