The Binomial Distribution

The name “The Binomial Distribution” is derived from the binomial expansion, because if you use the formula for binomial expansion,

you can substituteandand then the probability of obtainingsuccesses inattempts is given by theth term

There are three conditions necessary for the binomial to be a possible distribution.

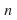1. is a fixed number. There are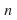trials or attempts.

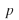2. is fixed throughout the process.

3. Each trial is independent of any other trial.

The notation for the Binomial distribution is

Example: A fair dice is thrown 10 times. Find the probability of

a)Throwing 3 sixes.

b)Throwing at most 1 six.

c)Throwing at least 1 six.

a)The probability of throwing a six isto 4dp.

b)to 4 dp.

c)to 4 dp.

Intuitively, ifattempts take place and the probability of success isthe expected number of successes is