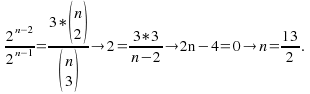The binomial Theorem allows us to expand many brackets without multiplying each bracket out one by one. It states:
To expand
we could expand
which would be a very long winded process. Or we could just substitute for
and
into the expression for the binomial expansion. Example: Expand
then
which simplifies to
and further to
We may be asked to solve questions involving the coefficients. For example, the coefficient of
in the binomial expansion of
is equal to 3 times the coefficient of
.Find n.
Using the binomial expansion, the coefficient ofis
Using the binomial expansion, the coefficient ofis
Hence we can write down the equation
Now we have to perform some trickery:
