Rrational numbers are fractions where both numerator and denominator are integers. Irrational numbers are conversely, any number that cannot be written as a fraction with one integer divided by another.
Suppose then we want to prove that
is irrational. We can prove this by contradiction.
Suppose that
where both
and
are numbers and suppose thatandhave no factors in common, so cannot be simplified. If
could be simplified thencould written
where
and
and relabelled
Square both sides ofto give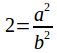
and multiply both sides by
to obtain
(1)
This means thatmust be even, sinceis a whole number so
is even.
This means we can write
where
is an integer, so that (1) becomes
Cancelling 2 from both sides gives
(2)
This means thatmust be even, sinceis an integer so
is even.
Write
and subsitute into (2) to give
Cancelling 2 from both sides gives
hence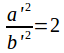
and
this is a contradiction since it is an assumption thatcannot be simplified, so thatis irrational.