Energy of an Orbiting Satellite

The gravitational potential energy of an orbiting satellite of mass m is given by(1) whereis the mass of the Earth.

We can find an expression for the kinetic energy by considering the equation for a satellite in a circular orbit. For such a satellite,  centripetal force = gravitational force.

There are equations for each of these forces.

The equation for the centripetal force is

The equation for the gravitational force is

=mass of satellite.

=Mass of Earth.

=radius of orbit

It is the universal gravitational constant, often called 'big g'.

We can equate these to obtainSimplifying gives

The kinetic energy is then(2)

Adding (1) and (2) gives the total energy.

(3)

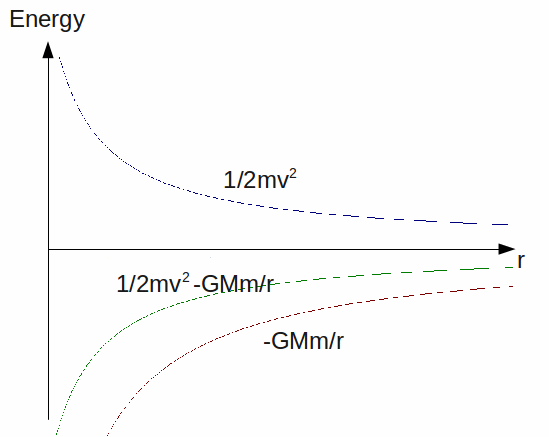
To move from a radiusto a radiussome energy must be given to the satellite. The gravitational potential energy will increase (become less negative) and the kinetic energy will decrease, but the new kinetic energy will still be positive and have the magnitude of the (negative) gravitational potential energy.

The total energy will always be described by (3).