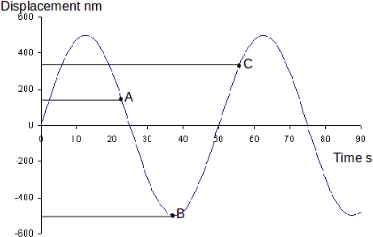
We can through, find the amplitude, frequency and angular frequency from the graph then estimate the velocity and acceleration by calculation. Suppose we have the waveform below and we want to fin the velocity and acceleration at points A, B and C.
\[x=A sin \omega t\]
, the velocity is \[v= \omega \sqrt{A^2- x^} \\]
and the acceleration is \[a= - \omega^2 x\]
.From the diagram above
\[A=500nm\]
and the period is \[T=50 s\]
frequency is \[f=1/50=0.02 \; Hz\]
, so the angular frequency is \[\omega = 2 \pi f = 2 \pi / 50= 0.04 \pi \]
.At A,
\[x \simeq 150 nm\]
so \[v= \omega \sqrt{A^2- x^2}= 0.04 \pi \sqrt{500^2-150^2}=56.11 nm/s=5.611 \times 10^{-8} m/s\]
\[a=- \omega^2 x \simeq =-(0.04 \pi)^2 \times 150nm/w = -2.369 nm/s^2=-2.369 \times 10^{-9} m/s^2 \]
At B,
\[x \simeq 500 nm\]
so \[v= \omega \sqrt{A^2- x^2}= 0.04 \pi \sqrt{500^2-500^2}=0 m/s\]
\[a=- \omega^2 x \simeq =-(0.04 \pi)^2 \times -500nm = 7.896 nm/s^2=7.896 \times 10^{-9} m/s^2 \]
At C,
\[x \simeq 350 nm\]
so \[v= \omega \sqrt{A^2- x^2}= 0.04 \pi \sqrt{500^2-350^2}=44.87 nm/s=4.487 \times 10^{-8} m/s\]
\[a=- \omega^2 x \simeq =-(0.04 \pi)^2 \times 350nm = -5.527 nm/s^2=-5.527 \times 10^{-9} m/s^2 =\]
