\[x\]
.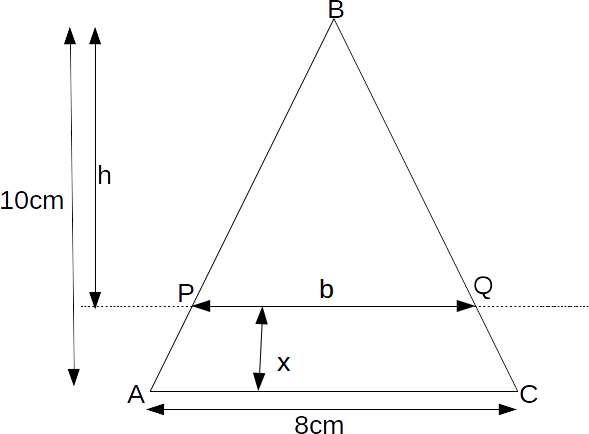
\[\frac{h}{b}=\frac{10}{8} \rightarrow h=\frac{5b}{4}\]
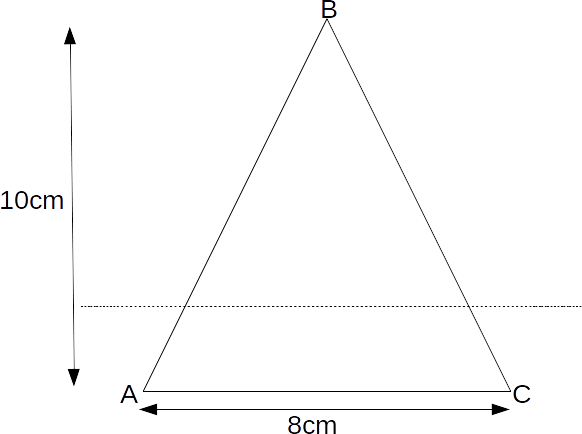
The area of triangle ABC is
\[\frac{8} \times 10=40\]
and the area of triangle PBQ is half of this, so \[\frac{1}{2}b \times h=20 \rightarrow bh=40\]
We now have simultaneous equations,
\[h=\frac{5b}{4}, \: hb=40\]
.Substitute the second of these into the first to give
\[\frac{5b}{4} \times b =40 \rightarrow b^2 =\frac{40}{5/4}=32 \rightarrow b =\sqrt{32}=4 \sqrt{2}\]
.Then
\[h=\frac{5b}{4}= \frac{5 \times 4 \sqrt{2}}{4}=5 \sqrt{2}\]
.Then
\[x=10-5 \sqrt{2}=5(2- \sqrt{2})\]
. 